ПУС (полимеры, усиленные стекловолокном) пултрузионные профили все больше используются в мостовых и гражданских сооружениях как альтернатива традиционным материалам из-за своих нескольких подходящих свойств которые включают высокую прочность, низкий собственный вес, быстрое время монтажа, низкие требования к эксплуатации и увеличенный ресурс. Несмотря на эти преимущества, есть несколько факторов, мещающих широкому распространению ПУС пултрузионных профилей в гражданском строительстве. Один из них – это недостаток широко общепринятых проектных норм. Данная статья описывает результаты аналитических, экспериментальных и цифровых исследований работы конструкций ПУС пултрузионных профилей, целью этого было оценить относительную точность существующих методов проектирования. Впервые предоставляется обзор доступных аналитических формул и рекомендация по проектированию ПУС пултрузионных изгибаемых элементов на оба, рабочее и максимальное, предельное состояние. Позже, результаты программы испытаний проведенной Высшим Техническим Институтом в Испании были кратко обсуждаемы – эксперименты включали тесты характеристик материала и полномасштабные тесты на изгиб двухтавтровой свободноопертой балки и консоли.
Эти тесты учли анализ поведения при эксплуатации ПУС изгибаемых элементов и наиболее характерные для них алгоритмы разрушений и соответствующих предельных нагрузок. Результаты экспериментальных тестов были сопоставлены с полученными из аналитически формул и числовых моделей в целях оценки относительной точности существующих методов расчета.
Ограниченных срок службы конструкций, сделанных из традиционных материалов и стоимость их последующего ремонта, которая существенно увеличивается в последние несколько лет, стимулирует развитие новых строительных материалов, которые менее подвержены коррозии, легче и проще монтировать. В этих обстоятельствах, за два последних десятилетия, ПУС материалы вообще и ПУС пултрузионные профили в частности, нашли увеличивающееся число применений в зданиях и мостах, как и в новых сооружениях, так и при реконструкции изношенной инфраструктуры. ПУС пултрузионные профили имеют большие перспективы как конструктивный материал, демонстрирующий несколько преимуществ перед традиционными материалами из-за своего высокого отношения прочности к весу, низкому собственному весу, электромагнитной прозрачности, возможности производства любых сечений, простоты в установке и неприхотливости в эксплуатации и увеличенном сроке службы в агрессивных средах. Помехой, в добавок к начальным капиталовложениям, недостатку конкурентоспособности для большинства применений и озабоченности относительно их работы под воздействием огня, служит то, что все еще нет широко принятых проектных норм или инструкций доступных для практикующих инженеров-проектировщиков. Как следствие, сейчас, большинство строительных проектов опирается на проектные пособия производителей, которые зачастую неполные и слишком осторожные.
Выпущенный в 1996 году Eurocomp Design Code and Handbook, содержит проектные советы в общем для композитных полимеров, но это не нормативный документ не обращает особого внимания на пултрузионные элементы. Европейский комитет по стандартизации (European Committee for Standardization –CEN) выпустил стандарт EN13706, нормативный документ который просто определяет два класса пултрузионного профиля (сопровождающейся минимальными оценками свойств материала), не предоставляя каких-либо проектных указаний. Итальянский Национальный Исследовательский Совет (Italian National Research Council) в 2007 году выпустил первые проектные указания для конструкций, сделанных из пултрузионных профилей, однако эти технические условия обязательны только в Италии. Также стоит упомянуть, что большинство книг по механике композитных материалов и композитных конструкций ссылаются на аэрокосмическое и машиностроительное инженерное применение – за исключением недавней публикации БАНК ЛС (BANK LC), которая предоставила полный набор правил проектирования для ПУС структур, написанных в формате гражданского строительства.
До того как полный и общепринятый набор проектный норм и советов может быть принят для использования ПУС пултрузионных профилей, дальнейшая исследовательская работа должна основываться на глубоком понимании работы конструкции и давать дополнительные подтверждения предложенным методам проектирования.
Данная статья содержит результаты аналитических, экспериментальных и числовых исследований работы конструкции ПУС пултрузионных профилей, целью которых было оценить относительную точность существующих методов проектирования. Впервые представляется обзор аналитических формул, которые были предложены для проектирования ПУС пултрузионных изгибаемых элементов на оба, рабочую и максимальную, предельное состояние. Позже, результаты программы испытаний проведенных в IST были кратко обсуждены – эксперименты включали тесты свойств материалов на мелкомасштабных пробных образцах и полномасштабные тесты на изгиб двутавровой свободноопертой ПУС балки и консоли. Эти тесты, детально описанные в источнике (18,19), позволили оценить поведение при эксплуатации ПУС изгибаемых элементов и некоторых из их распространенных алгоритмов разрушения и соответствующих предельных нагрузок. Результаты этих экспериментальных тестов позже сравнивались с прогнозами, полученными из аналитических формул и цифровых моделей для оценки относительной точности существующих методов проектирования.
Методы проектирования ПУС изгибаемых элементов.
Проектирование конструкций сделанных из ПУС пултрузионных профилей может выполняться в целом таким же способом как и стальные конструкции, предусмотрев приняв во внимание некоторые важные особенности, самой важной из которых является ортотропная природа и линейная упругая работа ПУС материала.
Соответственно, строительное проектирование стандартных ПУС профилей может выполняться на основе как и аналитической балочной модели, так и метода конечных пространственных или/и каркасных элементов. Как приблизительный образец, который наиболее часто сейчас принмается в расчете ПУС рам и ферм, применяется упрощенный эквивалент изотропной работы. При последующем приближении, ортотропная природа ПУС материала детально учтена.
Временные предельные нагрузки.
Для расчета предельных эксплуатационных нагрузок, прогиб пултрузионных изгибаемых элементов может определятся с достаточной точностью с помощью аналитической модели, основанной на теории балок Тимошенко, которая, учитывает влияние сдвига на общую деформацию. В сущности, деформация сдвига может быть относительно важной из-за соотношения модуля упругости-к-сдвигу. Для примера, упругий краткосрочный прогиб свободно опертой балки с сосредоточенной нагрузкой в середине пролета (схожие с балками эксперименты над которыми описаны ниже) может быть посчитан по формуле (1).
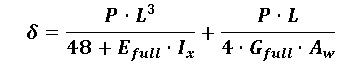
где,
δ- прогиб в середине пролета;
P-приложенная нагрузка;
L-длина пролета;
Ix- момент инерции сечения относительно оси X;
AW – площадь сечения;
Efull и Gfull – натурные продольные модули упругости и сдвига при эквивалентноц изотропной работе, которые могут быть определены экспериментально (см. следующий параграф).
В целях оценки длительных прогибов в пултрузионных балках, важно правильно исследовать вязкоупругую характеристику, связанную с полимерной природой вяжущего. Поэтому, времязависимые деформации из-за постоянных нагрузок должны рассчитываться принимая во внимания вязкоэластичные значения натурных модулей формулы (1). BANK LC приводит ряд модулей ползучести и экспоненты скорости ползучести рекомендуемые для расчета, которые были получены в ходе длительных испытаний на ползучесть применяя линеаризованную версию теории ползучести Финдли (Findley).
Состояния предела прочности
Для расчета состояния предела прочности, то обстоятельство, что ПУС изгибаемые элементы могут теоретически разрушится из-за нескольких признаках отказов должен приниматься в расчет. Для наиболее распространенных сечений (тонкостенное открытое сечение), могут быть следующие механизмы деформаций: (a) разрушение при изгибе (растяжение или сжатие); (b) разрушение при срезе стенки; (с) разрушение поперечной стенки; (d) местный прогиб; (e) поперечно-крутящий изгиб.
Разрушение при изгибе
Изгибающий момент, связанный с разрушением при изгибе пултрузионного элемента (Mu) может быть вычислен по формуле (2):
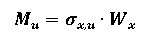
где,
σ_(x,u) — напряжение продольного разрушения (как и сжатия так и растяжения) ПУС материала;
Wx – модуль упругости поперечного сечения по сильной оси;
Стоит отметить, что разрушение при изгибе, из-за раздавливания при сжатии или разрыве при растяжении, мало вероятно что произойдет для большинства распространенных видов пултрузионных профилей, за исключением местного прогиба предотвращенного соответствующим укреплением.
Разрушение при срезе
Критическое срезающее усилие (Vu) пултрузионных изгибаемы элементов может быть вычислено по формуле (3):
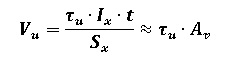
где,
τ_u- сопротивление плоскому сдвигу пултрузионного материала;
Sx – статический момент сечения относительно оси;
t- толщина (полки/стенки);
Av –площадь эпюр где, для большинства распространенных профилей, совпадает с площадью профиля.
Нужно отметить, что схожее с разрушением при изгибе разрушение при срезе материала стенки из-за напряжений плоского сдвига встречаются редко, так как сопротивление рассматриваемого поперечного сечения и пролетов привосходит явлением продольного изгиба.
Поперечное разрушение стенки
Стенка ПУС пултрузионной балки может разрушится из-за поперечного разрушения в основных двух местах: (a) в точке опирания и (b) в точке приложения нагрузки. Критическую разрушающую силу (F_u^crush) можно определить по формуле (4):
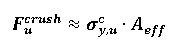
где,
σ_(y,u)^c- может быть взята как поперечное сопротивление сжатию
Aeff – эффективное сечение стенки подвергнутой приложению нагрузки, которая является площадью стенки прямо подвергнутой реакции опоры или приложенной нагрузки. Для того чтобы избежать этот механизм разрушения, длина опоры или пятна приложения нагрузки может быть увеличена и, вдобавок, могут применяться усилители стенок.